Abstraction Layer¶

Component Classes and Parameters¶

The main building block of the Abstraction Layer is the ComponentClass. The ComponentClass is intended to package together a collection of objects that relate to the definition of a model (e.g. cells, synapses, synaptic plasticity rules, random spike trains, inputs). All equations and event declarations that are part of particular entity model, such as neuron model, belong in a single ComponentClass. A ComponentClass can be used to represent either a specific model of a neuron or a composite model, including synaptic mechanisms.

The interface is the external view of the ComponentClass that defines what inputs and outputs the component exposes to other ComponentClass elements and the parameters that can be set for the ComponentClass. The interface consists of instances of ports and Parameter (see [fig:component_class_overview]).

ComponentClass Overview

As well as being able to specify the communication of continuous values, ComponentClass elements are also able to specify the emission and the reception of events. Events are discrete notifications that are transmitted over event ports. Since Event ports have names, saying that we transmit ‘event1’ for example would mean transmitting an event on the EventPort called ‘event1’. Events can be used for example to signal action potential firing.

ComponentClass¶

Attribute	Type/Format	Required
name	identifier	yes

Children	Multiplicity	Required
Parameter	set	no
AnalogSendPort	set	no
AnalogReceivePort	set	no
AnalogReducePort	set	no
EventSendPort	set	no
EventReceivePort	set	no
[Dynamics,ConnectionRule,RandomDistribution]	singleton	yes

A ComponentClass is composed of:

Parameter objects for the ComponentClass, which specify which values are required to be provided in the User Layer.
An unordered collection of port objects, which either publish or read state variables or derived values published from other components in the case of analog send and receive ports, or emit events or listen for events emitted from components. EventSendPort and EventReceivePort objects raise and listen for events passed between dynamic components.
A ‘main’ block, which specifies the nature of the component class:
- Dynamics, the component class defines a dynamic element such as neutron or post-synaptic response.
- ConnectionRule, the component class defines a rule by which populations are connected in projections.
- RandomDistribution, the component class defines random distribution.

Name attribute¶

Each ComponentClass requires a name attribute, which should be a valid and uniquely identify the ComponentClass in the document scope.

Parameter¶

Attribute	Type/Format	Required
name	identifier	yes
dimension	Dimension.name	yes

Parameter objects are placeholders for numerical values within a ComponentClass. They define particular qualities of the model, such as the firing threshold, reset voltage or the decay time constant of a synapse model. By definition, Parameters are set at the start of the simulation, and remain constant throughout.

Name attribute¶

Each Parameter requires a name attribute, which is a valid and uniquely identifies the Parameter within the ComponentClass.

Dimension attribute¶

Parameter elements must have a dimension attribute. This attribute specifies the dimension of the units of the quantity that is expected to be passed to the Parameter and should refer to the name of a Dimension element in the document scope. For a dimensionless parameters a Dimension with all attributes of power 0 can be used.

Mathematical Expressions¶

As of NineML version 1.0, only inline mathematical expressions, which have similar syntax to the ANSI C89 standard, are supported. In future versions it is envisaged that inline expressions will be either augmented or replaced with MathML (http://mathml.org) expressions.

MathInline¶

Body format	Required
Inline-maths expression	yes

MathInline blocks are used to specify mathematical expressions. Depending on the context, MathInline blocks should return an expression that evaluates to either a bool (when used as the trigger for OnCondition objects) or a real number (when used as a right-hand-side for Alias, TimeDerivative and StateAssignment objects). All numbers/variables in inline maths expressions are assumed to be real numbers.

Body¶

The following arithmetic operators are supported in all inline maths expressions and have the same interpretation and precedence levels as in the ANSI C89 standard,

Addition +
Subtraction -
Division /
Multiplication *

The following inequality and logical operators are only supported in inline maths expressions within Trigger elements. They also have the same interpretation and precedence levels as in ANSI C89 standard.

Greater than >
Lesser than <
Logical And: &&
Logical Or: ||
Logical Not: !

The following functions are built in and are defined as per ANSI C89:

exp(x)
sin(x)
cos(x)
log(x)
log10(x)
pow(x, p)
sinh(x)
cosh(x)
tanh(x)
sqrt(x)
atan(x)
asin(x)
acos(x)
asinh(x)
acosh(x)
atanh(x)
atan2(x)

The following symbols are built in, and cannot be redefined,

pi
t

where \(pi\) is the mathematical constant \(\pi\), and \(t\) is the elapsed simulation time within a Dynamics block.

The following random distributions are available in StateAssignment elements via the random namespace, :

random.uniform (see http://uncertml.org/distributions/uniform)
random.normal (see http://uncertml.org/distributions/normal)
random.binomial(N,P) (see http://uncertml.org/distributions/binomial)
random.poisson(L) (see http://uncertml.org/distributions/poisson)
random.exponential(L) (see http://uncertml.org/distributions/exponential)

Alias¶

Attribute	Type/Format	Required
name	identifier	yes

Children	Multiplicity	Required
MathInline	singleton	yes

An alias corresponds to an alternative name for a variable or part of an expression.

Aliases are motivated by two use cases:

substitution: rather than writing long expressions for functions of state variables, we can split the expressions into a chain of Alias objects, e.g.:
```
m_alpha = (alphaA + alphaB * V)/(alphaC + exp((alphaD + V / alphaE)))
m_beta = (betaA + betaB * V)/(betaC + exp((betaD + V / betaE)))
minf = m_alpha / (m_alpha + m_beta)
mtau = 1.0 / (m_alpha + m_beta)
dm/dt = (1 / C) * (minf - m) / mtau
```
In this case, m_alpha, m_beta, minf and mtau are all alias definitions. There is no reason we couldn’t expand our \(\mathrm{d}m/\mathrm{d}t\) description out to eliminate these intermediate Alias objects, but the expression would be very long and difficult to read.
Accessing intermediate variables: if we would like to communicate a value other than a simple StateVariable to another ComponentClass. For example, if we have a component representing a neuron, which has an internal StateVariable, ‘V’, we may be interested in transmitting a current, for example \(i=g*(E-V)\).

Name attribute¶

Each Alias requires a name attribute, which is a valid and uniquely identifies the Alias from all other elements in the ComponentClass.

Constant¶

Attribute	Type/Format	Required
name	identifier	yes
units	Unit.symbol	yes

Body format	Required
`float`	yes

Constant objects are used to specify physical constants such as the Ideal Gas Constant (i.e. 8.314462175 JK\(^{-1}\)mol\(^{-1}\)) or Avogadro’s number (i.e. 6.0221412927\(\times\)10\(^{23}\)mol\(^{-1}\)), and to convert unit dimensions between abstract mathematical quantities.

The use of Constant elements to hold fixed model parameters is strongly discouraged since this breaks the division of semantic layers (abstraction and user), which is a key feature of NineML (see [sec:scope]).

Name attribute¶

Each Constant requires a name attribute, which should be a valid and uniquely identify the Dimension in current the scope.

Units attribute¶

Each Constant requires a units attribute. The units attribute specifies the units of the property and should refer to the name of a Unit element in the document scope.

Body¶

Any valid numeric value, including shorthand scientific notation e.g. 1e-5 (\(1\times10^{-5}\)).

Ports¶

Ports allow components to communicate with each other during a simulation. Ports can either transmit discrete events or continuous streams of analog data. Events are typically used to transmit and receive spikes between neutron model, whereas analog ports can be used to model injected current and gap junctions between neuron models.

Ports are divided into sending, EventSendPort and AnalogSendPort, and receiving objects, EventReceivePort, AnalogReceivePort and AnalogReducePort. With the exception of AnalogReducePort objects, each receive port must be connected to exactly one matching (i.e. analog\(\to\)analog, event\(\to\)event) send port, where as a send port can be connected any number of receive ports. AnalogReducePort objects can be connected to any number of AnalogSendPort objects; the values of the connected ports are then “reduced” to a single data stream using the operator provided to the AnalogReducePort.

AnalogSendPort¶

Attribute	Type/Format	Required
name	[StateVariable,Alias].name	yes
dimension	Dimension.name	yes

AnalogSendPort objects allow variables from the current component to be published externally so they can be read by other ComponentClass objects. Each AnalogSendPort can be connected to multiple AnalogReceivePort and AnalogReducePort objects.

Name attribute¶

Each AnalogSendPort requires a name attribute, which should refer to a StateVariable or Alias within the current ComponentClass.

Dimension attribute¶

Each AnalogSendPort requires a dimension attribute. This attribute specifies the dimension of the units of the quantity that is expected to be passed through the AnalogSendPort and should refer to the name of a Dimension element in the document scope.

AnalogReceivePort¶

Attribute	Type/Format	Required
name	identifier	yes
dimension	Dimension.name	yes

AnalogReceivePorts allow variables that have been published externally to be used within the current component. Each AnalogReceivePort must be connected to exactly one AnalogSendPort.

Name attribute¶

Each AnalogReceivePort requires a name attribute, which is a valid and uniquely identifies the AnalogReceivePort from all other elements in the ComponentClass.

Dimension attribute¶

Each AnalogReceivePort requires a dimension attribute. This attribute specifies the dimension of the units of the quantity that is expected to be passed through the AnalogReceivePort and should refer to the name of a Dimension element in the document scope.

AnalogReducePort¶

Attribute	Type/Format	Required
name	identifier	yes
dimension	Dimension.name	yes
operator	+	yes

Reduce ports can receive data from any number of AnalogSendPort objects (including none). An AnalogReducePort takes an additional operator compared to an AnalogReceivePort, operator, which specifies how the data from multiple analog send ports should be combined to produce a single value. Currently, the only supported operation is \(+\), which calculates the sum of the incoming port values.

The motivation for AnalogReducePort is that it allows us to make our ComponentClass definitions more general. For example, if we are defining a neuron, we would define an AnalogReducePort called InjectedCurrent. This allows us to write the membrane equation for that neuron as

\(\mathrm{d}V/\mathrm{d}t = (1/C) * InjectedCurrent\).

Then, when we connect this neuron to synapses, current-clamps, etc, we simply need to connect the send ports containing the currents of these ComponentClass_es to the InjectedCurrent reduce port, without having to change our original ComponentClass definitions.

Name attribute¶

Each AnalogReducePort requires a name attribute, which is a valid and uniquely identifies the AnalogReducePort from all other elements in the ComponentClass.

Dimension attribute¶

Each AnalogReducePort requires a dimension attribute. This attribute specifies the dimension of the units of the quantity that is expected to be communicated through the AnalogReducePort and should refer to the name of a Dimension element in the document scope.

Operator attribute¶

Each AnalogReducePort requires an operator attribute. The operator reduces the connected inputs to a single value at each time point. For example the following port,

<AnalogReducePort name="total_membrane_current" dimension="current" operator="+"/>

will take all of the electrical currents that have been connected to it via AnalogSendPorts and sum them to get the total current passing through the membrane.

EventSendPort¶

Attribute	Type/Format	Required
name	identifier	yes

An EventSendPort specifies a channel over which events can be transmitted from a component. Each EventSendPort can be connected any number of EventReceivePort objects.

Name attribute¶

Each EventSendPort requires a name attribute, which is a valid and uniquely identifies the EventSendPort from all other elements in the ComponentClass.

EventReceivePort¶

Attribute	Type/Format	Required
name	identifier	yes

An EventReceivePort specifies a channel over which events can be received by a component. Each EventReceivePort must be connected to exactly one EventSendPort.

Name attribute¶

Each EventReceivePort requires a name attribute, which is a valid and uniquely identifies the EventReceivePort from all other elements in the ComponentClass.

Dynamic Regimes¶

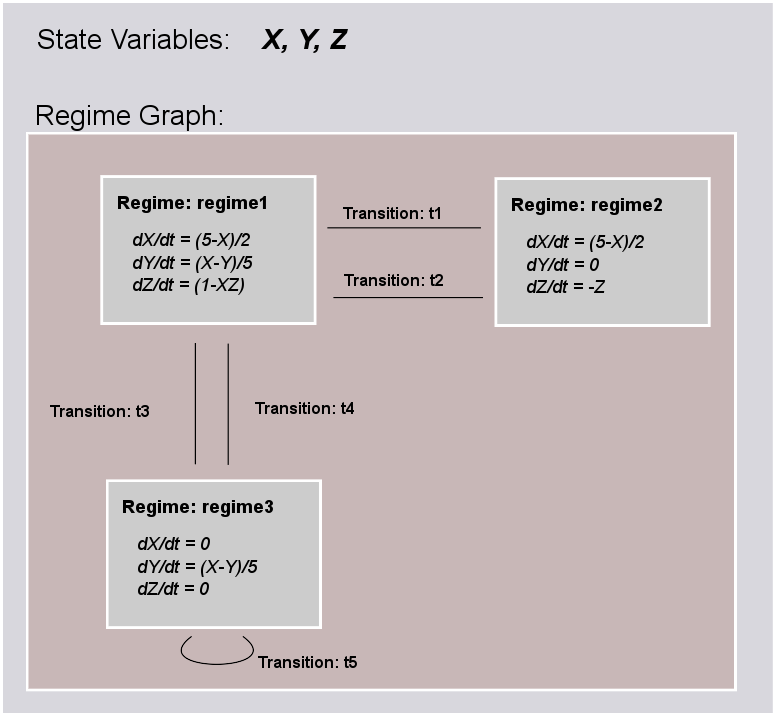
Dynamics blocks define the dynamic equations of models such as neurons, post-synaptic responses or plasticity of synaptic weights. In Dynamics blocks, state variables are evolved by one or more sets of ordinary differential equations (ODE). Each set of equations is called a regime, and only one regime can be active at a particular point in time. The currently active regime can be changed by a transition event, which is represented as a logical expression on the state variables. When the logical expression evaluates to true, the transition must occur.

[fig:simple_regime_graph] illustrates a hypothetical transition graph for a system with three state variables, \(X\), \(Y\) and \(Z\), which transitions between three ODE regimes, regime1, regime2 and regime3. At any time, the model will be in one and only one of these regimes, and the state variables will evolve according to the ODE of that regime.

The dynamics block for an example component.

Dynamics¶

Children	Multiplicity	Required
StateVariable	set	no
Regime	set	yes
Alias	set	no
Constant	set	no

The Dynamics block represents the internal mechanisms governing the behaviour of the component. These dynamics are based on ordinary differential equations (ODE) but may contain non-linear transitions between different ODE regimes. The regime graph (e.g. [fig:simple_regime_graph]) must contain at least one Regime element, and contain no regime islands. At any given time, a component will be in a single regime, and can change which regime it is in through transitions.

Note

Alias objects are defined in Dynamics blocks, not Regime blocks. This means that aliases are the same across all regimes.

StateVariable¶

Attribute	Type/Format	Required
name	identifier	yes
dimension	Dimension.name	yes

The state of the model is defined by a set of StateVariable objects. The value of a StateVariable can change in two ways:

continuously through TimeDerivative elements (in Regime elements), which define how the StateVariable evolves over time, e.g. \(dX/dt=1-X\).

discretely through StateAssignment (in OnCondition or OnEvent transition elements), which make discrete changes to a StateVariable value, e.g. \(X = X + 1\).

Name attribute¶

Each StateVariable requires a name attribute, which is a valid and uniquely identifies the StateVariable from all other elements in the ComponentClass.

Dimension attribute¶

Each StateVariable requires a dimension attribute. This attribute specifies the dimension of the units of the quantities that StateVariable is expected to be initialised and updated with and should refer to the name of a Dimension element in the document scope.

Regime¶

Attribute	Type/Format	Required
name	identifier	yes

Children	Multiplicity	Required
TimeDerivative	set	no
OnCondition	set	no
OnEvent	set	no

A Regime element represents a system of ODEs in time on StateVariable. As such, Regime defines how the state variables change (propagate in time) between subsequent transitions.

Name attribute¶

Each Regime requires a name attribute, which is a valid and uniquely identifies the Regime from all other elements in the ComponentClass.

TimeDerivative¶

Attribute	Type/Format	Required
variable	StateVariable.name	yes

Children	Multiplicity	Required
MathInline	singleton	yes

TimeDerivative elements contain a mathematical expression for the right-hand side of the ODE

\[\frac{\mathrm{d} variable}{\mathrm{d} t} = expression\]

which can contain of references to any combination of StateVariable, Parameter, AnalogReceivePort, AnalogReducePort and Alias elements with the exception of aliases that are derived from RandomDistribution components. Therefore, only one TimeDerivative element is allowed per StateVariable per Regime. If a TimeDerivative for a StateVariable is not defined in a Regime, it is assumed to be zero.

Variable attribute¶

Each TimeDerivative requires a variable attribute. This should refer to the name of a StateVariable in the ComponentClass. Only one TimeDerivative is allowed per variable in each Regime.

Transitions¶

The currently active dynamic regime can be changed via transitions. Transitions have instantaneous temporal extent (i.e. they are event-like). There are two types of transitions, condition-triggered transitions (see OnCondition), which are evoked when an associated trigger expression becomes true, or event-triggered transitions (see OnEvent), which are evoked when an associated event port receives an event from an external component. Multiple state assignments can be defined and multiple events can be sent within a single transition block.

During either type of transition three instantaneous actions can occur:

The component transitions to a target regime (can be the same as the current regime)
State variables can be assigned new values (see StateAssignment)
The component can send events (see OutputEvent).

There is no order defined in transitions; this means that the order of resolution of state assignments can be ambiguous. If, for example, we have two transitions, T1 and T2, originating from the same Regime, in which T1 contains the state assignment V=V+1 and T2 contains the assignment V=V*V, and both transitions are triggered simultaneously, then there is no guarantee about the value of V. It is left to the user to ensure such situations do not occur. Implementations should emit a warning when they are detected.

OnCondition¶

Attribute	Type/Format	Required
target_regime	Regime.name	no

Children	Multiplicity	Required
Trigger	singleton	yes
StateAssignment	set	no
OutputEvent	set	no

OnCondition blocks are activated when the mathematical expression in the Trigger block becomes true. They are typically used to model spikes in spiking neuron models, potentially emitting spike events and/or transitioning to an explicit refractory regime.

Target_regime attribute¶

An OnEvent can have a target_regime attribute, which should refer to the name of a Regime element in the ComponentClass that the dynamics block will transition to when the trigger condition is met. If the target_regime attribute is omitted the regime will transition to itself.

OnEvent¶

Attribute	Type/Format	Required
target_regime	Regime.name	no
port	EventReceivePort.name	yes

Children	Multiplicity	Required
StateAssignment	set	no
OutputEvent	set	no

OnEvent blocks are activated when the dynamics component receives an event from an external component on the port the OnEvent element is “listening” to. They are typically used to model the transient response to spike events from incoming synaptic connections.

Cascading of events, i.e. events triggering subsequent events, are permitted, which in theory could be recursive through components depending on their connectivity. It is the user’s responsibility to ensure that infinite recursion does not occur with zero delay. Implementations may decide to terminate after a given number of recursive cascades of zero delay (say 1000) to prevent infinite loops, but such limits should be modifiable by the user.

Port attribute¶

Each OnEvent requires a port attribute. This should refer to the name of an EventReceivePort in the ComponentClass interface.

Target_regime attribute¶

OnEvent can have a targetRegime attribute, which should refer to the name of a Regime element in the ComponentClass that the dynamics block will transition to when the OnEvent block is triggered by an incoming event. If the targetRegime attribute is omitted the regime will transition to itself.

Trigger¶

Children	Multiplicity	Required
MathInline	singleton	yes

Trigger objects define when an OnCondition transition should occur. The MathInline block of a Trigger can contain any arbitrary combination of ‘and’, ‘or’ and ‘negation’ logical operations (‘\(\&\&\)’, ‘\(||\)’ and ‘\(!\)’ respectively) on the result of pure inequality relational operations (‘\(>\)’ and ‘\(<\)’), which follow the syntax and semantics of ANSI C89. The inequality expression may contain references to StateVariable, AnalogReceivePort, AnalogReducePort, Parameter and Alias elements, with the exception of Alias elements derived from random distributions. The OnCondition block is triggered when the boolean result of the Trigger statement changes from false to true.

StateAssignment¶

Attribute	Type/Format	Required
variable	StateVariable.name	yes

Children	Multiplicity	Required
MathInline	singleton	yes

StateAssignment elements allow discontinuous changes in the value of state variables. Only one state assignment is allowed per variable per transition block. The assignment expression may contain references to StateVariable, AnalogReceivePort, AnalogReducePort, Parameter and Alias elements, including Alias elements derived from random distributions. State assignments are typically used to reset the membrane voltage after an outgoing spike event or update post-synaptic response states after an incoming spike event.

Variable attribute¶

Each StateAssignment requires a variable attribute. This should refer to the name of a StateVariable in the ComponentClass. Only one StateAssignment is allow per variable in each OnEvent or OnCondition block.

OutputEvent¶

Attribute	Type/Format	Required
port	EventSendPort.name	yes

OutputEvent elements specify events to be raised during a transition. They are typically used to raise spike events from within OnCondition elements.

Port attribute¶

Each OutputEvent requires a port attribute. This should refer to the name of an EventSendPort in the ComponentClass interface.

Random Distributions¶

Values for a property across all elements in a container (e.g. cells in a population, post-synaptic responses, plasticity rules or delays in a projection) can be defined as a random distribution by a Component within a RandomDistribution_Value element. A random distribution component must parameterize a ComponentClass with a RandomDistribution block; the component class defines the random distribution family (e.g. normal, cauchy, gamma, etc…). As of version 1.0, the only random distributions available to the user are those defined in the standard library, however, derived distributions are planned for future versions.

RandomDistribution¶

Attribute	Type/Format	Required
standard_library	URL	yes

The names and parameters of the random distribution in the standard library match the UncertML definitions that can be found at http://www.uncertml.org/distributions. The subset of the UncertML distributions that should be implemented are by NineML compliant packages are,

BernoulliDistribution
BetaDistribution
BinomialDistribution
CauchyDistribution
ChiSquareDistribution
DirichletDistribution
ExponentialDistribution
FDistribution
GammaDistribution
GeometricDistribution
HypergeometricDistribution
LaplaceDistribution
LogisticDistribution
LogNormalDistribution
MultinomialDistribution
NegativeBinomialDistribution
NormalDistribution
ParetoDistribution
PoissonDistribution
UniformDistribution
WeibullDistribution

Note

Note: C implementations of these distributions are available in the GNU Scientific Library, http://www.gnu.org/software/gsl/

Standard_library attribute¶

The standard_library attribute is required and should point to a URLin the http://www.uncertml.org/distributions/ directory.

Network Connectivity¶

The connection rule for cells in the source and destination populations of a Projection (i.e. the rule that determines which source cells are connected to which destination cells) is defined by a connection-rule component within the Connectivity element of the Projection. This component must parameterize a ComponentClass with a ConnectionRule block, which describes the connection algorithm. As of version 1.0, the only connection rules available to the user are those defined in the standard library (e.g. all-to-all, one-to-one, probabilistic, etc…), however, custom connectivity rules are planned for future versions.

ConnectionRule¶

Attribute	Type/Format	Required
standard_library	URL	yes

Connection rules must be one of 6 standard library types, all-to-all, one-to-one, probabilistic, explicit, random-fan-out and random-fan-in, provided to the standard_libarary attribute.

Note

In future versions, built-in connectivity rules are to be replaced with mathematically expressed connection rules.

Standard_library attribute¶

The standard_library attribute is required and should point to the URLin the http://nineml.net/9ML/1.0/connectionrules/directory that corresponds to the desired connection rule.

All cells in the source population are connected to all cells in the destination population.

Each cell in the source population is connected to the cell in the destination population with the corresponding index. Note that this requires that the source and destination populations be the same size.

All cells in the source population are connected to cells in the destination population with a probability defined by a parameter, which should be named probability. The properties supplied to the probability parameter should either be a SingleValue representing the probability of a connection between all source and destination cell pairs, or a ArrayValue or ExternalArrayValue of size \(M{\times}N\), where \(M\) and \(N\) are the size of the source and destination populations respectively. For array probabilities, the data in the ArrayValue or ExternalArrayValue are ordered by the indices

\[i_{\mathrm{prob}} = i_{\mathrm{source}} * N_{\mathrm{dest}} + i_{\mathrm{dest}}\]

where \(i_{\mathrm{prob}}\), \(i_{\mathrm{source}}\) and \(i_{\mathrm{dest}}\) are the indices of the probability entry, and the source and destination cells respectively, and \(N_{\mathrm{dest}}\) is the size of the destination population.

Cells in the source population are connected to cells in the destination population as specified by an explicit arrays. The source and destination are defined via parameters, which should be named sourceIndicies and destinationIndicies parameters respectively.

The properties supplied to the sourceIndicies parameter should be a ArrayValue or ExternalArrayValue drawn from the set \(\{1,\ldots,M\}\) where \(M\) is the size of the source population and be the same length as the property supplied to the target-indices parameter.

The properties supplied to the destinationIndicies parameter should be a ArrayValue or ExternalArrayValue drawn from the set \(\{1,\ldots,N\}\) where \(N\) is the size of the source population and be the same length as the property supplied to the source-indices parameter.

Each cell in the source population is connected to a fixed number of randomly selected cells in the destination population. The number of cells is specified by the parameter number. The property supplied to the number parameter should be a SingleValue.

Each cell in the destination population is connected to a fixed number of randomly selected cells in the source population. The number of cells is specified by the parameter number. The property supplied to the number parameter should be a SingleValue.